Basado en el planteamiento de este artículo: https://medium.com/atg-analytical/que-nos-deparar%C3%A1-el-coronavirus-548f3b87ebcd

En resumen, estamos prediciendo el número de muertes en el Reino Unido para los próximos 5 días basándonos en 3 grupos de factores:

• Propagación (20 y 15 días antes de la predicción)
• Total de muertes (10 y 5 días antes de la predicción)
• Días desde que comienza la propagación comunitaria, contando el día 0 = 10 días antes de que el número total de muertes llegue a 5 (el mismo día de la predicción)

De esta forma podemos predecir al menos 5 días, o incluso más si añadimos nuestras muertes predichas a los datos, pero eso sería una predicción basada en otras predicciones, así que para empezar simplemente haremos esta predicción de 5 días.

Empecemos a explicar el cuaderno. En primer lugar, importando las librerías básicas que necesitaremos más adelante. Estas son simplemente pandas, para dar forma a nuestros dataframes, bokeh, que es la librería que utilizo para la representación gráfica y algunos módulos matemáticos.

import pandas as pd 
from bokeh.models import ColumnDataSource, Range1d, LabelSet, Label
from bokeh.plotting import figure, output_file, show
from bokeh.models import ColumnDataSource, Range1d, LabelSet, Label
from bokeh.plotting import figure, output_file, show
from bokeh.layouts import gridplot
import numpy as np
import math
import urllib
from numpy import inf

Nuestros datos se importan del ECDC, y permite descargarlos desde script, por lo que podemos mantener actualizado el cuaderno.

link = ‘https://covid.ourworldindata.org/data/ecdc/full_data.csv'
urllib.request.urlretrieve(link, ‘Descargas/full_data.csv’)

Antes de entrar en materia, es necesario explorar los datos. Aquí creo diferentes marcos de datos para los países a los que quiero echar un vistazo, donde compruebo sus tasas de mortalidad, propagación, defunción, etc.

Data = pd.read_csv(‘Descargas/full_data.csv’).fillna(0)
SpainCases = Data[Data[‘location’]==’Spain’].drop(‘location’, axis=1)
ItalyCases = Data[Data[‘location’]==’Italy’].drop(‘location’, axis=1)
ChinaCases = Data[Data[‘location’]==’China’].drop(‘location’, axis=1)
GermanyCases = Data[Data[‘location’]==’Germany’].drop(‘location’, axis=1)
FranceCases = Data[Data[‘location’]==’France’].drop(‘location’, axis=1)
UKCases = Data[Data[‘location’]==’United Kingdom’].drop(‘location’, axis=1)
KoreaCases = Data[Data[‘location’]==’South Korea’].drop(‘location’, axis=1)
SpainMortality = SpainCases[‘total_deaths’][-1:]/SpainCases[‘total_cases’][-1:]*100
ItalyMortality = ItalyCases[‘total_deaths’][-1:]/ItalyCases[‘total_cases’][-1:]*100
ChinaMortality = ChinaCases[‘total_deaths’][-1:]/ChinaCases[‘total_cases’][-1:]*100
GermanyMortality = GermanyCases[‘total_deaths’][-1:]/GermanyCases[‘total_cases’][-1:]*100
FranceMortality = FranceCases[‘total_deaths’][-1:]/FranceCases[‘total_cases’][-1:]*100
UKMortality = UKCases[‘total_deaths’][-1:]/UKCases[‘total_cases’][-1:]*100
KoreaMortality = KoreaCases[‘total_deaths’][-1:]/KoreaCases[‘total_cases’][-1:]*100
Mortality = np.hstack([SpainMortality, ItalyMortality, ChinaMortality, GermanyMortality, FranceMortality, UKMortality, KoreaMortality]) 
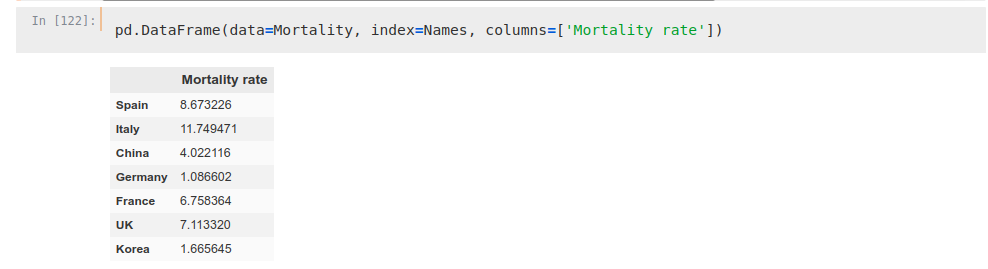
Names = np.hstack([‘Spain’, ‘Italy’, ‘China’, ‘Germany’, ‘France’, ‘UK’, ‘Korea’])

Podemos ver cómo las tasas de mortalidad son muy diferentes entre países para ser tenidas en cuenta en un análisis, por lo que sólo tendremos en cuenta las defunciones como marcador.

Las variables de propagación son:

• Estado de las escuelas
• Sucesos masivos
• Estado de alarma
• Transporte público
• Ejercicio en espacios públicos
• Comercios abiertos
• Calidad del sistema sanitario

Concedemos valores diferentes a cada uno de estos factores en función del momento y del país. Por ejemplo, a pesar de que Italia y España tienen unos de los sistemas sanitarios más bestias del mundo, los valoro igual que valoro la respuesta china a la epidemia debido a los enormes esfuerzos realizados por ellos.

Este trozo de código es idéntico para cada país, modificando únicamente los valores de fecha y calidad en función de sus condiciones. Para que la explicación de esta parte del código no sea demasiado larga sólo mostraré un R0 y un país. Estamos utilizando tres factores de propagación diferentes (2.5, 2 y 1.5) para cada país para ver cual funciona mejor.

Como se ha dicho antes, elegimos como día 0 el 10 días anterior al momento en que hay 5 deths acumulados en un país.

Spain = SpainCases[SpainCases.index>(SpainCases[SpainCases['total_deaths']>5].index-10)[0]]

Ahora, creamos nuestro R0

R0_1_Spain = [2.5]

Y añadimos a nuestro dataframe estos valores que hemos elegido para las medidas tomadas por el gobierno, multiplicándolos por nuestra tasa de propagación.

El caso español por ejemplo es bastante fácil, ya que todas las medidas se tomaron básicamente el mismo día (la alarma estatal empezó el 15 de marzo, antes básicamente no se tomaron medidas). Las clases en todo el país se cerraron ese día pero las zonas del país más afectadas habían cerrado colegios y universidades antes, aproximadamente el 10 de marzo tras el cierre de Madrid, que es el foco principal de la epidemia en España por lo que tomaremos esa fecha.

Multiplicamos nuestra tasa de propagación por el valor que hayamos elegido. También creamos un recuento de «Días».

Spain_1 = Spain
Spain_1['dia'] = np.arange(0, len(Spain))
Spain_1['Clases'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-09'])), 1), np.full((len(Spain[Spain['date']>'2020-03-09'])), 0.25)]) 
Spain_1['Eventos_masivos'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-14'])), 1), np.full((len(Spain[Spain['date']>'2020-03-14'])), 0.25)]) 
Spain_1['Estado_de_Alarma'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-14'])), 1), np.full((len(Spain[Spain['date']>'2020-03-14'])), 0.25)]) 
Spain_1['Transporte_publico'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-14'])), 1), np.full((len(Spain[Spain['date']>'2020-03-14'])), 0.5)]) 
Spain_1['Ejercicio_en_publico'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-14'])), 1), np.full((len(Spain[Spain['date']>'2020-03-14'])), 0.25)]) 
Spain_1['Tiendas_abiertas_al_publico'] = R0_1_Spain*np.hstack([np.full((len(Spain[Spain['date']<='2020-03-14'])), 1), np.full((len(Spain[Spain['date']>'2020-03-14'])), 0.25)]) 
Spain_1['Medical_Quality'] = R0_1_Spain*np.hstack([np.full((len(Spain)), 0.25)])
Spain_1 = Spain_1.fillna(0)

Ahora, tenemos una aproximación (¡probablemente no muy buena!) de las tasas de propagación en cada momento. Obtenemos una función geométrica usando esos factores, almacenándolos en arrays numpy, y luego sustituimos los datos en el DataFrame:

Prop_1Clases = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Clases.append(Prop_1Clases[-1]*Spain_1['Clases'][Spain_1.index[0]+i])
Prop_1Eventos = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Eventos.append(Prop_1Eventos[-1]*Spain_1['Eventos_masivos'][Spain_1.index[0]+i] )
Prop_1Alarma = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Alarma.append(Prop_1Alarma[-1]*Spain_1['Estado_de_Alarma'][Spain_1.index[0]+i])
Prop_1Transprte = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Transprte.append(Prop_1Transprte[-1]*Spain_1['Transporte_publico'][Spain_1.index[0]+i])
Prop_1Ejercicio = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Ejercicio.append(Prop_1Ejercicio[-1]*Spain_1['Ejercicio_en_publico'][Spain_1.index[0]+i])
Prop_1Tiendas = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Tiendas.append(Prop_1Tiendas[-1]*Spain_1['Tiendas_abiertas_al_publico'][Spain_1.index[0]+i])
Prop_1Medical = [10]
for i in np.arange(0, len(Spain_3)-1):
    Prop_1Medical.append(Prop_1Medical[-1]*Spain_1['Medical_Quality'][Spain_1.index[0]+i])    
    
Spain_1.drop(['Clases', 'Eventos_masivos', 'Eventos_masivos', 'Estado_de_Alarma', 'Transporte_publico', 'Ejercicio_en_publico', 'Tiendas_abiertas_al_publico', 'Medical_Quality'], axis=1, inplace=True)            
Spain_1['Clases'] = Prop_1Clases
Spain_1['Eventos_masivos'] = Prop_1Eventos
Spain_1['Estado_de_Alarma'] = Prop_1Alarma
Spain_1['Transporte_publico'] = Prop_1Transprte
Spain_1['Ejercicio_en_publico'] = Prop_1Ejercicio
Spain_1['Tiendas_abiertas_al_publico'] = Prop_1Tiendas
Spain_1['Medical_Quality'] = Prop_1Medical

Hacemos esto para cada tasa de propagación y para cada país, obteniendo marcos de datos similares a éste:

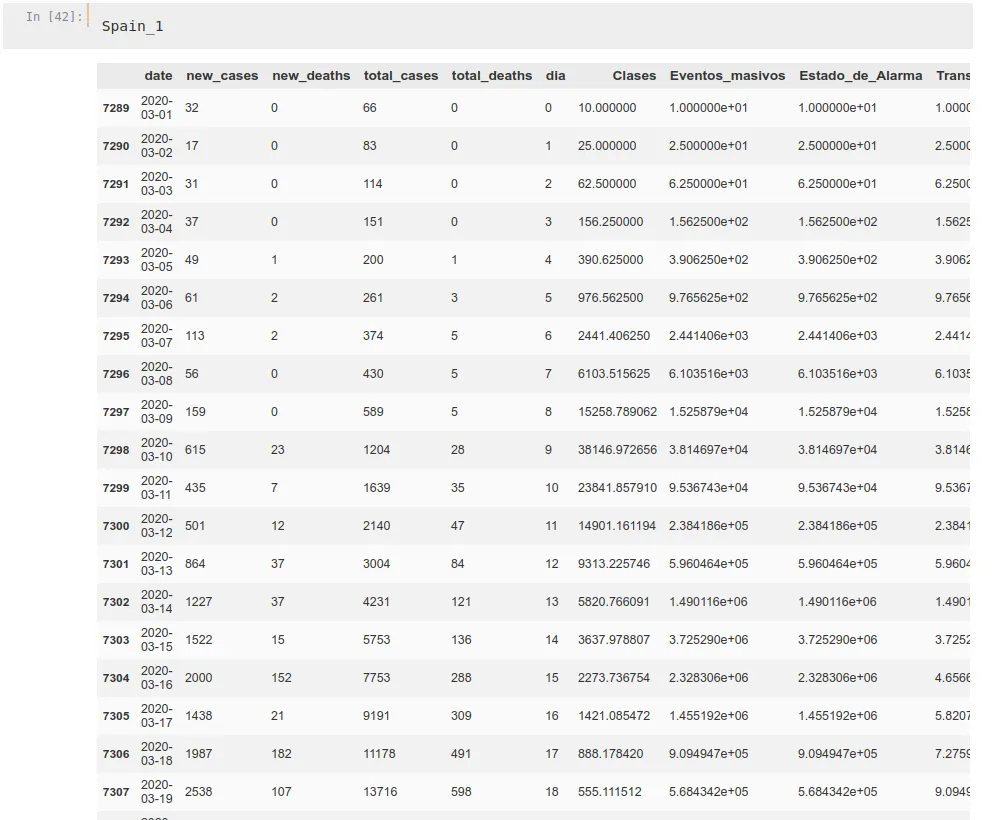
Ahora que ya tenemos listos nuestros marcos de datos por país, los apilamos. Agregamos los datos de propagación por un lado y los datos de muertes por otro, apilando los países uno a uno. Primero, China, luego Italia, España y, por último, Reino Unido, que será el que intentaremos predecir.

Apilamos estos datos dos veces, obteniendo un retardo de 20 días por un lado y un retardo de 15 días por otro. Las columnas de datos de propagación son ‘[6, 7, 8, 9, 10, 11, 12]’ y apilamos verticalmente cada país. A pesar de que este trozo de código pueda parecer largo no es más que una iteración del mismo código todo el tiempo.

Stack_1_1RO_1 = np.vstack([China_1.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_1.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_1_1RO_2 = np.vstack([China_2.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_2.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_1_1RO_3 = np.vstack([China_3.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_3.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_1_2RO_1 =  Spain_1.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_1_2RO_2 =  Spain_2.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_1_2RO_3 =  Spain_3.iloc[:-20, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_1_3RO_1 = np.vstack((Stack_1_1RO_1,Stack_1_2RO_1))
Stack_1_3RO_2 = np.vstack((Stack_1_1RO_2,Stack_1_2RO_2))
Stack_1_3RO_3 = np.vstack((Stack_1_1RO_3,Stack_1_2RO_3))
Stack_1_4RO_1 =  UK_1.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_1_4RO_2 =  UK_2.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_1_4RO_3 =  UK_3.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_1_5RO_1 = np.vstack((Stack_1_3RO_1,Stack_1_4RO_1))
Stack_1_5RO_2 = np.vstack((Stack_1_3RO_2,Stack_1_4RO_2))
Stack_1_5RO_3 = np.vstack((Stack_1_3RO_3,Stack_1_4RO_3))
Stack_2_1RO_1 = np.vstack([China_1.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_1.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_2_1RO_2 = np.vstack([China_2.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_2.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_2_1RO_3 = np.vstack([China_3.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/60, Italy_3.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/61])
Stack_2_2RO_1 =  Spain_1.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_2_2RO_2 =  Spain_2.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_2_2RO_3 =  Spain_3.iloc[5:-15, [6, 7, 8, 9, 10, 11, 12]].values/47
Stack_2_3RO_1 = np.vstack((Stack_2_1RO_1,Stack_2_2RO_1))
Stack_2_3RO_2 = np.vstack((Stack_2_1RO_2,Stack_2_2RO_2))
Stack_2_3RO_3 = np.vstack((Stack_2_1RO_3,Stack_2_2RO_3))
Stack_2_4RO_1 =  UK_1.iloc[10:-10, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_2_4RO_2 =  UK_2.iloc[10:-10, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_2_4RO_3 =  UK_3.iloc[10:-10, [6, 7, 8, 9, 10, 11, 12]].values/67
Stack_2_5RO_1 = np.vstack((Stack_2_3RO_1,Stack_2_4RO_1))
Stack_2_5RO_2 = np.vstack((Stack_2_3RO_2,Stack_2_4RO_2))
Stack_2_5RO_3 = np.vstack((Stack_2_3RO_3,Stack_2_4RO_3))
Prop1 = np.hstack((Stack_1_5RO_1, Stack_2_5RO_1))
Prop2 = np.hstack((Stack_1_5RO_2, Stack_2_5RO_2))
Prop3 = np.hstack((Stack_1_5RO_3, Stack_2_5RO_3))

Especial atención al hecho de que estamos dividiendo los datos de propagación y muerte por los millones de personas que cada país tiene como población, por lo que tenemos una propagación ajustada a cada país. A pesar de que China tiene una población mucho mayor, estamos utilizando 60 millones de personas como medida, ya que es aproximadamente la población de la provincia de Hubei, foco principal de la epidemia.

Las muertes pasan por el mismo proceso, sólo que esta vez es la columna 4 y los datos se toman entre 10 y 5 días antes de la predicción.

Stack_3_1RO_1 = np.vstack([China_1.iloc[10:-10, [4]].values/60, Italy_1.iloc[10:-10, [4]].values/61])
Stack_3_1RO_2 = np.vstack([China_2.iloc[10:-10, [4]].values/60, Italy_2.iloc[10:-10, [4]].values/61])
Stack_3_1RO_3 = np.vstack([China_3.iloc[10:-10, [4]].values/60, Italy_3.iloc[10:-10, [4]].values/61])
Stack_3_2RO_1 =  Spain_1.iloc[10:-10, [4]].values/47
Stack_3_2RO_2 =  Spain_2.iloc[10:-10, [4]].values/47
Stack_3_2RO_3 =  Spain_3.iloc[10:-10, [4]].values/47
Stack_3_3RO_1 = np.vstack((Stack_3_1RO_1,Stack_3_2RO_1))
Stack_3_3RO_2 = np.vstack((Stack_3_1RO_2,Stack_3_2RO_2))
Stack_3_3RO_3 = np.vstack((Stack_3_1RO_3,Stack_3_2RO_3))
Stack_3_4RO_1 =  UK_1.iloc[15:-5, [4]].values/67
Stack_3_4RO_2 =  UK_2.iloc[15:-5, [4]].values/67
Stack_3_4RO_3 =  UK_3.iloc[15:-5, [4]].values/67
Stack_3_5RO_1 = np.vstack((Stack_3_3RO_1,Stack_3_4RO_1))
Stack_3_5RO_2 = np.vstack((Stack_3_3RO_2,Stack_3_4RO_2))
Stack_3_5RO_3 = np.vstack((Stack_3_3RO_3,Stack_3_4RO_3))
Stack_4_1RO_1 = np.vstack([China_1.iloc[15:-5, [4]].values/60, Italy_1.iloc[15:-5, [4]].values/61])
Stack_4_1RO_2 = np.vstack([China_2.iloc[15:-5, [4]].values/60, Italy_2.iloc[15:-5, [4]].values/61])
Stack_4_1RO_3 = np.vstack([China_3.iloc[15:-5, [4]].values/60, Italy_3.iloc[15:-5, [4]].values/61])
Stack_4_2RO_1 =  Spain_1.iloc[15:-5, [4]].values/47
Stack_4_2RO_2 =  Spain_2.iloc[15:-5, [4]].values/47
Stack_4_2RO_3 =  Spain_3.iloc[15:-5, [4]].values/47
Stack_4_3RO_1 = np.vstack((Stack_4_1RO_1,Stack_4_2RO_1))
Stack_4_3RO_2 = np.vstack((Stack_4_1RO_2,Stack_4_2RO_2))
Stack_4_3RO_3 = np.vstack((Stack_4_1RO_3,Stack_4_2RO_3))
Stack_4_4RO_1 =  UK_1.iloc[20:, [4]].values/67
Stack_4_4RO_2 =  UK_2.iloc[20:, [4]].values/67
Stack_4_4RO_3 =  UK_3.iloc[20:, [4]].values/67
Stack_4_5RO_1 = np.vstack((Stack_4_3RO_1,Stack_4_4RO_1))
Stack_4_5RO_2 = np.vstack((Stack_4_3RO_2,Stack_4_4RO_2))
Stack_4_5RO_3 = np.vstack((Stack_4_3RO_3,Stack_4_4RO_3))
Cases1 = np.hstack((Stack_3_5RO_1, Stack_4_5RO_1))
Cases2 = np.hstack((Stack_3_5RO_2, Stack_4_5RO_2))
Cases3 = np.hstack((Stack_3_5RO_3, Stack_4_5RO_3))

Mismo método para los días

Stack_5_1RO_1 = np.vstack([China_1.iloc[20:, [5]].values, Italy_1.iloc[20:, [5]].values])
Stack_5_1RO_2 = np.vstack([China_2.iloc[20:, [5]].values, Italy_2.iloc[20:, [5]].values])
Stack_5_1RO_3 = np.vstack([China_3.iloc[20:, [5]].values, Italy_3.iloc[20:, [5]].values])
Stack_5_2RO_1 = Spain_1.iloc[20:, [5]].values
Stack_5_2RO_2 = Spain_2.iloc[20:, [5]].values
Stack_5_2RO_3 = Spain_3.iloc[20:, [5]].values
Stack_5_3RO_1 = np.vstack((Stack_5_1RO_1,Stack_5_2RO_1))
Stack_5_3RO_2 = np.vstack((Stack_5_1RO_2,Stack_5_2RO_2))
Stack_5_3RO_3 = np.vstack((Stack_5_1RO_3,Stack_5_2RO_3))
Stack_5_4RO_1 = UK_1.iloc[20:, [5]].values
Stack_5_4RO_2 = UK_2.iloc[20:, [5]].values
Stack_5_4RO_3 = UK_3.iloc[20:, [5]].values
Days1 = np.vstack((Stack_5_3RO_1,Stack_5_4RO_1))
Days2 = np.vstack((Stack_5_3RO_2,Stack_5_4RO_2))
Days3 = np.vstack((Stack_5_3RO_3,Stack_5_4RO_3))

Nuestro Y…

Stack_6_1RO_1 = np.vstack([China_1.iloc[20:, [2]].values/60, Italy_1.iloc[20:, [2]].values/61])
Stack_6_1RO_2 = np.vstack([China_2.iloc[20:, [2]].values/60, Italy_2.iloc[20:, [2]].values/61])
Stack_6_1RO_3 = np.vstack([China_3.iloc[20:, [2]].values/60, Italy_3.iloc[20:, [2]].values/61])
Stack_6_2RO_1 =  Spain_1.iloc[20:, [2]].values/47
Stack_6_2RO_2 =  Spain_2.iloc[20:, [2]].values/47
Stack_6_2RO_3 =  Spain_3.iloc[20:, [2]].values/47
Stack_6_3RO_1 = np.vstack((Stack_6_1RO_1,Stack_6_2RO_1))
Stack_6_3RO_2 = np.vstack((Stack_6_1RO_2,Stack_6_2RO_2))
Stack_6_3RO_3 = np.vstack((Stack_6_1RO_3,Stack_6_2RO_3))
Stack_6_4RO_1 =  UK_1.iloc[20:, [2]].values/67
Stack_6_4RO_2 =  UK_2.iloc[20:, [2]].values/67
Stack_6_4RO_3 =  UK_3.iloc[20:, [2]].values/67
Y1 = np.log10(np.vstack((Stack_6_3RO_1,Stack_6_4RO_1)))
Y2 = np.log10(np.vstack((Stack_6_3RO_2,Stack_6_4RO_2)))
Y3 = np.log10(np.vstack((Stack_6_3RO_3,Stack_6_4RO_3)))

Ahora, tenemos nuestros 3 factores X y nuestro Y, los apilamos juntos y los preprocesamos. Los datos de propagación y muertes crecen demasiado rápido, así que los convertimos a escala logarítmica al apilarlos.

Stackeo1 = np.log10(np.hstack((Prop1, Cases1)))
Stackeo2 = np.log10(np.hstack((Prop2, Cases2)))
Stackeo2 = np.log10(np.hstack((Prop3, Cases3)))
x1 = np.hstack((Stackeo1, Days1))
x2 = np.hstack((Stackeo2, Days2))
x3 = np.hstack((Stackeo2, Days3))

La conversión a escala logarítmica puede producir infinitos, convertimos estos -inf a 0 y luego normalizamos todas nuestras X’

x1[x1 == -inf] = 0
x2[x2 == -inf] = 0
x3[x3 == -inf] = 0
Y1[Y1 == -inf] = 0
Y2[Y2 == -inf] = 0
Y3[Y3 == -inf] = 0
from sklearn.preprocessing import MinMaxScaler
min_max_scaler1 = MinMaxScaler()
X1 = min_max_scaler1.fit_transform(x1)
min_max_scaler2 = MinMaxScaler()
X2 = min_max_scaler2.fit_transform(x2)
min_max_scaler3 = MinMaxScaler()
X3 = min_max_scaler3.fit_transform(x3)
min_max_scaler4 = MinMaxScaler()
Y1 = min_max_scaler4.fit_transform(Y1)
min_max_scaler5 = MinMaxScaler()
Y2 = min_max_scaler5.fit_transform(Y2)
min_max_scaler6 = MinMaxScaler()
Y3 = min_max_scaler6.fit_transform(Y3)

Vale, esto ha sido largo, lo sé, pero ya casi hemos terminado de preparar los datos. Finalmente, usamos un ExtraTreesRegressor junto con un SelectFromModel para ver cuál de todos estos datos que hemos reunido es más relevante para nuestra Y, y transformamos nuestra X a esas formas.

from sklearn.ensemble import ExtraTreesRegressor
from sklearn.feature_selection import SelectFromModel
RF = ExtraTreesRegressor()
RF.fit(X1, Y1)
featureselector1 = SelectFromModel(RF, prefit=True)
X1 = featureselector1.transform(X1)
RF = ExtraTreesRegressor()
RF.fit(X2, Y2)
featureselector2 = SelectFromModel(RF, prefit=True)
X2 = featureselector2.transform(X2)
RF = ExtraTreesRegressor()
RF.fit(X3, Y3)
featureselector3 = SelectFromModel(RF, prefit=True)
X3 = featureselector3.transform(X3)
Shape1 = X1.shape[1]
Shape2 = X2.shape[1]
Shape3 = X3.shape[1]

Como ahora estamos usando un LSTM, que es probablemente la herramienta más fuerte para hacer este tipo de trabajo, necesitamos obtener una matriz tridimensional, hecha de esta manera:

• Time steps
• Features
• Factors

Así pues, remodelamos nuestras X y dividimos nuestros datos en entrenamiento y prueba para cuantificar la calidad de los distintos modelos que vamos a probar.

X1_train = X1[:-10].reshape(len(X1)-10, 1, X1.shape[1])
X2_train = X2[:-10].reshape(len(X2)-10, 1, X2.shape[1])
X3_train = X3[:-10].reshape(len(X3)-10, 1, X3.shape[1])
X1_test = X1[-10:].reshape(10, 1, X1.shape[1])
X2_test = X2[-10:].reshape(10, 1, X2.shape[1])
X3_test = X3[-10:].reshape(10, 1, X3.shape[1])
Y1_train = Y1[:-10]
Y2_train = Y2[:-10]
Y3_train = Y3[:-10]
Y1_test = Y1[-10:]
Y2_test = Y2[-10:]
Y3_test = Y3[-10:]

Los modelos estarán compuestos por 5 capas, de las cuales 2 serán LSTM y 3 Densas, todas ellas utilizando funciones de activación ‘REctified Linear Unit’ (RELU) y probando tanto optimizaciones RMSProp como Adamax.

modelLSTM01_1 = Sequential()
modelLSTM01_1.add(LSTM(40, return_sequences=True))
modelLSTM01_1.add(LSTM(200, activation='relu'))
modelLSTM01_1.add(Dense(40, activation='relu'))
modelLSTM01_1.add(Dense(10, activation='relu'))
modelLSTM01_1.add(Dense(1, activation='relu'))
modelLSTM01_1.compile(optimizer='Adamax', loss='mae', metrics = ['mae'])
modelLSTM01_1.fit(X1_train, Y1_train, epochs=50, batch_size=1, verbose=1)
LSTMPredicton01_1 = modelLSTM01_1.predict(X1_test)
score, mae = modelLSTM01_1.evaluate(X1_test, Y1_test)
score = sqrt(mean_squared_error(LSTMPredicton01_1, Y1_test))
print('Test score:', score)
print('Accuracy:', mae)

Valoramos la precisión en la fase de prueba y en la fase de entrenamiento para seleccionar nuestro modelo. Hacemos esto con 6 modelos diferentes.

Esto sería básicamente todo. Ahora que hemos seleccionado nuestro modelo, para hacer nuestra predicción simplemente cambiamos nuestra X, seleccionando 5 días más sobre los datos de UK (u otro país), como podemos ver en nuestras siguientes fases del git, que no incluiré en este artículo para no alargarme.

Nuestros datos serán normalizados y logarítmicos. Podemos invertir estos haciendo:

10**(mix_max_scaler1.inverse_transform(LSTMPredicton01_1))

Lo que nos daría una estadística de muertes por millón.

Espero que este artículo sea lo suficientemente comprensible a pesar de su extensión.