Para hacer un problema de clasificación de imágenes, decidí hacer un pequeño experimento, comparando dos arquictecturas de Redes Neuronales diferentes, PyTorch y Tensorflow (usando Keras).

PyTorch es una librería de aprendizaje automático de código abierto desarrollada principalmente por el laboratorio de investigación de IA de Facebook (FAIR), mientras que TensorFlow fue desarrollado por el equipo de Google Brain para uso interno de Google, aunque hoy en día es de uso libre para cualquiera. Para un manejo más sencillo de TensorFlow, utilizo el framework Keras, que facilita la compleja gramática que utiliza TF.

Datos

For this experiment, we will be using the ‘MNIST’ dataset. It is a really large dataset (70.000 samples) of Para este experimento utilizaremos el conjunto de datos «MNIST». Se trata de un conjunto de datos realmente grande (70.000 muestras) de dígitos manuscritos. El conjunto de entrenamiento contiene 60.000 muestras, mientras que el conjunto de prueba contiene otras 10.000. Este conjunto de datos ya está integrado en la mayoría de los frameworks y está bastante extendido. Puede ver un ejemplo de este conjunto de datos en la siguiente figura.

TensorFlow

Empezaremos con TensorFlow. Empezamos cargando los datos

from keras import *(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()

Como se ha dicho antes, este conjunto de datos está incluido en el framework keras. Ahora, la forma de este tensor cargado es de 60000 muestras de 28×28, lo que hace un tensor tridimensional (60000, 28, 28). Podríamos usar una red convolucional, pero hacerlo así nos llevaría mucho tiempo. En su lugar, podemos convertir este tensor en un tensor bidimensional (60000, 28*28). Además, los datos vienen como datos de 256 bits, nos interesa normalizar estos datos, lo que podemos hacer simplemente dividiendo por 255 (ya que va de 0 a 255).

#Normalizing data
x_train = x_train.astype("float32") / 255
x_test = x_test.astype("float32") / 255
# Reshaping (60000, 28, 28) into (60000, 28*28)
x_train = x_train.reshape(x_train.shape[0], x_train.shape[1]* x_train.shape[1])
x_test = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[1])

Ahora, convertimos la parte «y» en categórica. En lugar de tener un único número representado (1, 2, 3…9) tenemos una matriz binaria en forma de 10, que representa esos números únicos mediante 0s y 1s.

num_classes = 10
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

Ahora, como decíamos antes utilizamos una red neuronal simple basada en ‘Dense’. Para este experimento probamos diferentes funciones de activación, optimizadores y combinaciones de capas.

Primero, 3 redes neuronales diferentes usando una red neuronal de 3 capas, usando la siguiente combinación:

model1 = Sequential()
model1.add(Dense(128, activation=’linear’))
model1.add(Dense(64, activation=’relu’))
model1.add(Dense(10, activation=’softmax’))

Para cada uno de ellos utilizamos un optimizador diferente. Normalmente, para muchos problemas utilizo Adamax o RMSprop como optimizadores, esta vez añado SGD. Para la medida de pérdida utilizo ‘categorical_crossentropy’ y para las métricas sobre pruebas utilizo ‘accuracy’.

model1.compile(optimizer=keras.optimizers.Adamax(lr=0.03), loss=’categorical_crossentropy’, metrics = [‘accuracy’])model2.compile(optimizer=keras.optimizers.RMSprop(lr=0.03), loss='categorical_crossentropy', metrics = ['accuracy'])model3.compile(optimizer=keras.optimizers.SGD(lr=0.03), loss='categorical_crossentropy', metrics = ['accuracy'])

Además, pruebo otra combinación de capas, añadiendo una cuarta capa, que quedaría así

model61 = Sequential()
model61.add(Dense(256, activation='relu'))
model61.add(Dense(128, activation='linear'))
model61.add(Dense(64, activation='relu'))
model61.add(Dense(10, activation='softmax'))model61.compile(optimizer=keras.optimizers.SGD(lr=0.03), loss='categorical_crossentropy', metrics = ['accuracy'])

En la literatura se recomienda utilizar softmax o funciones de activación similares para problemas de clasificación, se demuestra durante este ejercicio que las activaciones softmax en la última capa acaban obteniendo mejores resultados.

El mejor resultado global sería el siguiente:

model62 = Sequential()
model62.add(Dense(256, activation=’relu’))
model62.add(Dense(128, activation=’relu’))
model62.add(Dense(64, activation=’relu’))
model62.add(Dense(10, activation=’softmax’))
model62.compile(optimizer=keras.optimizers.SGD(lr=0.03), loss=’categorical_crossentropy’, metrics = [‘accuracy’])model62.fit(x_train, y_train, epochs=5, verbose=1, batch_size=20)
score = model62.evaluate(x_test, y_test, verbose=0)

Este modelo obtuvo un 97,5% (0,077 de entropía cruzada) y un 98% de precisión respectivamente en las fases de prueba y entrenamiento. El entrenamiento y la prueba de este modelo duraron 1’45», lo que es un resultado bastante decente, a pesar de que aquí sólo iteramos el modelo 5 veces. Utilizando 15 épocas en lugar de 5 obtenemos una precisión del 99,8% en el entrenamiento, pero la precisión en las pruebas sólo llega al 98%, por lo que probablemente se trate de un sobreajuste innecesario.

PyTorch

Ahora, para PyTorch seguimos más o menos los mismos caminos. Primero, importamos los datos (integrados en el framework de PyTorch también). PyTorch es un poco diferente, ya que tenemos que crear primero un transformador para establecer el tipo de datos que queremos tener, y luego obtener un trainloader y testloader (train=False/True).

# We import the data from 'datasets.MNIST', PyTorch allows us to directly normalize the data on the importation. To do that we setup a transformer that will create a normalized tensor ('transform').transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,)),])trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)trainloader = torch.utils.data.DataLoader(trainset, batch_size=20)testset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=False, transform=transform)testloader = torch.utils.data.DataLoader(testset, batch_size=20)

La utilidad dataloader de PyTorch nos permite diferenciar entre etiquetas y datos:

images, labels = next(iter(trainloader))

Las imágenes se cargan en iteraciones utilizando el cargador de trenes. Utilizando la función «vista», remodelamos los tensores en un tensor bidimensional.

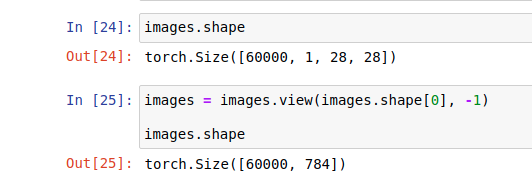
images = images.view(images.shape[0], -1)

Ahora que tenemos nuestros datos listos, podemos crear nuestro modelo. Los modelos creados tendrán estructuras similares a las que usamos en Keras (funciones de activación, optimizadores, capas…).

En primer lugar, definimos las capas de nuestro modelo, que serían algo así (los números se refieren a las formas entrantes y salientes).

model8 = nn.Sequential(nn.Linear(784, 256),
                      nn.ReLU(),
                      nn.Linear(256, 128),
                      nn.Softmax(),
                      nn.Linear(128, 64),
                      nn.ReLU(),
                      nn.Linear(64, 10))

Ahora, el criterio de pérdida y el optimizador.

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adamax(model8.parameters(), lr=0.003)

El modelo está configurado, ahora tenemos que entrenarlo y luego probar los resultados. Establecemos 5 iteraciones, y hacemos que se ejecute sobre el cargador. También tenemos que establecer ‘optimizer.zero_grad’ para hacer que los pesos se restablezcan y hacer que la retropropagación se ejecute utilizando ‘loss.backward’. La pérdida en el conjunto de entrenamiento se almacena en ‘running_loss’ que se imprime después de cada iteración que termina.

epochs = 5
for e in range(epochs):
    running_loss = 0
    for images, labels in trainloader:
        images = images.view(images.shape[0], -1)
    
        optimizer.zero_grad()
        
        output = model8(images)
        loss = criterion(output, labels)
        loss.backward()
        optimizer.step()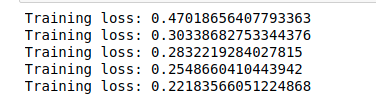

El mejor modelo obtuvo un error de entropía cruzada en la fase de entrenamiento de 0,10 (frente a sólo 0,0479 obtenido con Keras), por lo que parece que Keras ha superado a su homólogo PyTorch. Sin embargo, cuando comprobamos los informes de precisión (que podemos obtener con el siguiente fragmento de código), vemos que PyTorch obtuvo un sobresaliente 100% de precisión tanto en los conjuntos de entrenamiento como en los de prueba, frente al 98-97,5% de Keras utilizando el mismo número de iteraciones y tamaños de lote.

top_p, top_class = output.topk(1, dim=1)equals = top_class == labels.view(*top_class.shape)
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')

Podemos ver los resultados de PyTorch en este pequeño trozo de código, que nos permite comprobar gráficamente las etiquetas frente a las imágenes.

%matplotlib inline
import helperimages, labels = next(iter(trainloader))img = images[0].view(1, 784)logps = model8(img)ps = torch.exp(logps)
helper.view_classify(img.view(1, 28, 28), ps)

Si quieres los cuadernos utilizados en este pequeño experimento, puedes descargarlos de nuestro git: https://github.com/ATG-Analytical/Image-Classification.git