Los efectos de esta pandemia están siendo gravísimos y no podemos evitar mirar al futuro para saber cuando nuestra vida volverá a cierta normalidad.

Desde mi limitada experiencia y buscando el día en el que podamos salir decidimos hacer un estudio sobre la propagación de este virus, haciendo un modelo que prediga las consecuencias en los próximos días. Pasaré a dar algunas pinceladas sobre el planteamiento de este estudio.

Los datos que utilizaremos son los datos oficiales de la ECDC (European Centre for Disease Prevention and Control), descargables aqui: https://covid.ourworldindata.org/data/ecdc/total_cases.csv

Primero, ¿cómo vamos a medir el alcance de esta pandemia en cada país? A priori el dato que más atención se le podría dar es a los casos totales y diarios registrados.

Podemos seguir el siguiente razonamiento: El periodo de incubación de este virus se encuentra aproximadamente entre 2 y 10 días, siendo la mediana 5 y teniendo en cuenta el dato de que el 97.5% de los infectados habrán presentado síntomas antes de los 11 días. Entonces, podemos asumir grosso modo que los contagiados detectados hoy son personas que se infectaron hace 10 días. Ahora debemos añadir la siguiente parte, ¿cuánto tarda una persona en morir una vez presenta síntomas? Esto presenta muchas aristas: la carga vírica que ha recibido la persona, patologías previas, la “fortaleza” de esta persona, etc. En cualquier caso, vamos a asumir de nuevo una media de entre 5 y 10 días en las que una persona presenta síntomas hasta que muere.

En las siguientes dos imágenes podemos ver las muertes y los casos diarios registrados en Italia durante los últimos 27 días, primero los datos tal cual y luego aplicando un simple retardo de 5 días. Podemos apreciar como la correlación aumenta una vez hemos aplicado esta diferencia temporal.

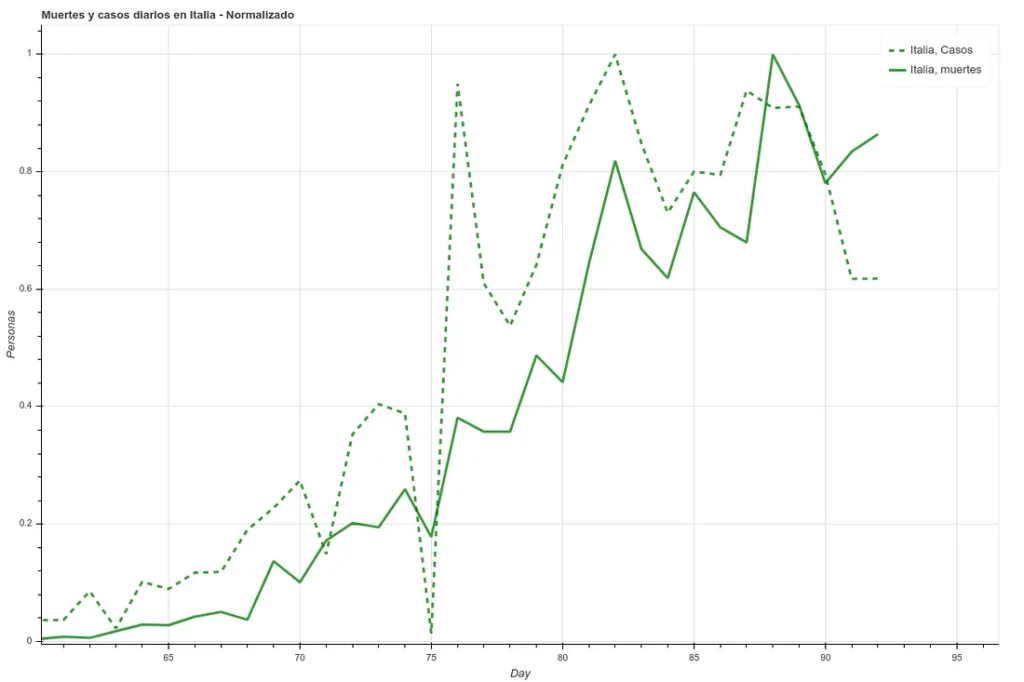
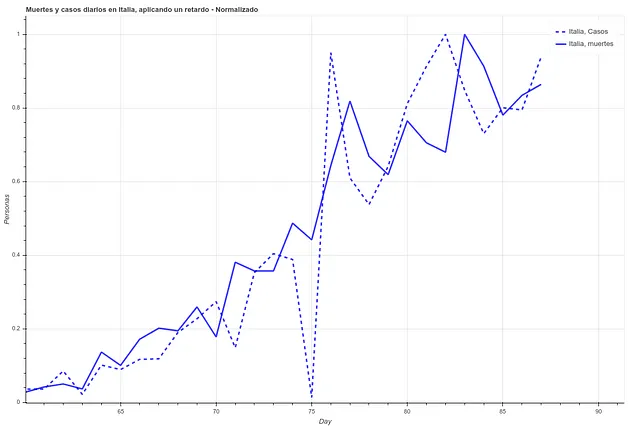
Sin embargo, aquí chocamos con un problema. Dado que cada país tiene índices de mortalidad muy diferentes (véase la tabla de mortalidad) no parece que podamos tomar la cantidad de contagios como un medidor fiable. España e Italia tienen dos de los mejores sistemas sanitarios del mundo (según la OMS, ambos países se encuentran en el ‘top 10’), sin embargo ambos países tienen las tasas de mortalidades más altas entre los países donde el contagio está más extendido.

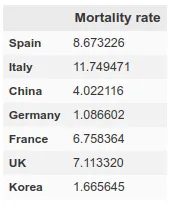
Esto nos indica que este virus está mucho más extendido de lo que nos dicen las cifras de contagiados, lo cuál podemos confirmar viendo algunos estudios (como éste producido por el departamento de epidemiología del Imperial College de Londres), que da cifras de millones de infectados en ambos países, aunque los datos oficiales dan datos de alrededor de 100k infectados a 1 de Abril que se escribe este artículo. Si se aplica la tasa de mortalidad de los países donde se han realizado tests de forma más extensiva como Alemania o Korea del Sur al número absoluto de muertos, obtenemos una cantidad de infectados en Italia y España superior al millón. El estudio del Imperial College que nombramos antes da datos para España de un 15% de la población infectada, lo cuál se traduce en más de 7 millones de infectados. Podemos ver una tabla con dichos resultados aquí.

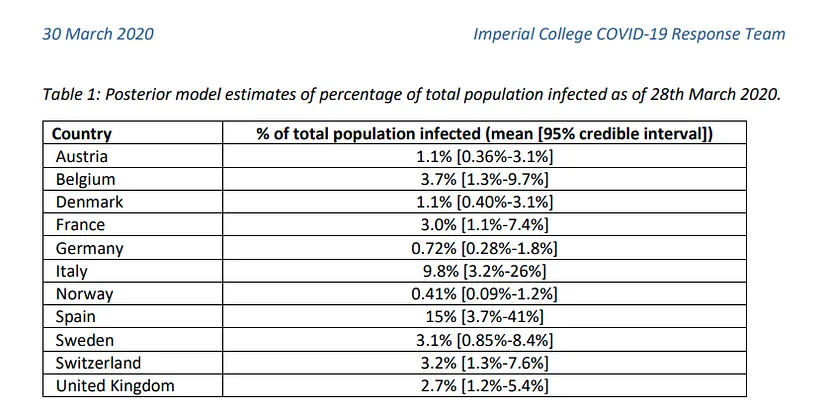
En cualquier caso, podemos ver como estas cifras oscilan en cantidades demasiado grandes como para utilizadas en un estudio de predicciones a menos que tengamos también el número de tests realizados por día, un número que no es facilitado en la mayoría de países. Por tanto, para ver la evolución de la pandemia nos centraremos en un dato más objetivo y medible, las muertes.

Tomaremos 3 tipos de factores diferentes. Por un lado, los factores de propagación. Se estima el factor de propagación medio del COVID19 entre 2.5 y 2. Esto es, el número de nuevas infecciones que crea una persona infectada. Este número podemos estimar que varia dada la sociabilidad de la gente (mayor en Italia o España) o las costumbres sociales (el trato cercano en estos dos países). También podríamos tener en cuenta que esas 2.5–2 infecciones no se darán en un mismo día. En cualquier caso, se podría discutir mucho cuál sería el número ideal, pero pondremos 3 factores geométricos para representar esto: 2.5, 2 y 1.5.

Creamos una función geométrica, esto es, que una función donde el elemento i-1 se multiplica por el mismo número siempre para producir un elemento i. Posteriormente, esta función se verá constreñida por los factores que afectan a su propagación.

Por visualizar esto (utilizando el factor de propagación 2.5):

Día 1: 10 persona infectada

Día 2: 10*2.5 = 25 personas infectadas

Día 3: 25*2.5 = 62.5 personas infectadas

Día 4: 62.5*2.5 = 156.25 personas infectadas

Ahora bien, esto es una propagación sin límites. En cierto momento, todos los gobiernos han realizado medidas de distanciamiento social, cancelado reuniones masivas de gente, establecido estados de alarma, etc. Con lo que añadimos a la anterior función un segundo parámetro. Supongamos que el día 5 desde el 0 el gobierno prohíbe las concentraciones de más de 5000 personas (medida que Francia tomó el 29 de Febrero, cuando contaba con 2 muertes totales). Vamos a suponer esto como un factor 0.5.

Día 5: 156.25*2.5*0.5 = 195.33

Día 6: 195.33*2.5*0.5 = 244.15

Se ha ralentizado la propagación. Ahora hacemos esto para una serie de factores diferentes y establecemos estas series para varios países. Abajo podemos ver el ejemplo de China, donde se decretó la alarma y se canceló todo tipo de eventos donde hubiera contagio social el día 12 tras el contagio.

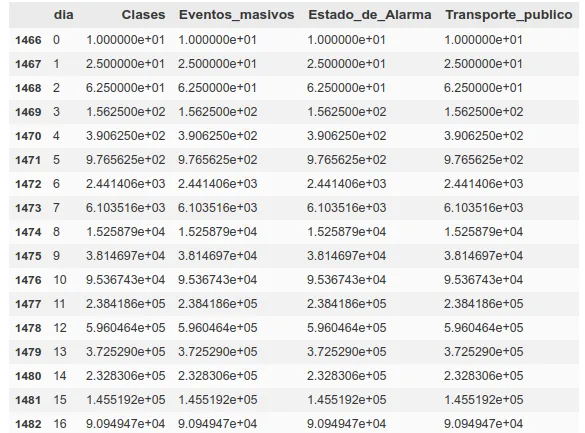
Como comentamos anteriormente, de la infección a la muerte estamos estableciendo aproximadamente 20 días desde el día 0 (~5-10 de incubación, ~5-10 de enfermedad), por lo que para calcular las muertes hoy, usaremos los datos de propagación de hace 20–15 días.

En esa misma tabla podemos ver como el primer factor es el día. Tomaremos los días pasados desde un ‘día 0’, que consideraremos será 10 días anterior a alcanzar un total de 5 muertes en dicha región, de forma que podamos establecer ese día 0 como un comienzo del contagio comunitario.

Por último, el número de contagios no parece un factor particularmente fiable. Para sustituirlo, usaremos el número absoluto de muertes entre 5 y 10 días previo al día que queremos calcular, de modo que tengamos una cierta medida de lo inmerso que está el virus en esa sociedad.

Tenemos por tanto 3 tipos de factores diferentes:

• Número total de muertes hace 5–10 días
• Propagación esperada del virus hace 20–15 días (para diferentes factores, estado de alarma, transporte público, ejercicio en público, tiendas abiertas al público, clases abiertas)
• Días pasados desde el inicio de contagio comunitario

Los juntamos todos, obteniendo finalmente 17 factores diferentes, de los cuales serán 2 de muertes, 1 de la cuenta diaria y 14 de propagación (los de propagación y muertes están doblados, tomando los datos de dos temporalidades diferentes, 10–5 y 20–15).

Los factores que crecen a gran escala como el número total de muertes y las tasas de propagación son pasadas a escala logarítmica y divididos por la población de cada país, lo cual facilitará su manejo más tarde y nos dan una visión más realista del crecimiento relativo para cada caso. Además, tras pasarlos a escala logarítmica, normalizamos los datos para que el algoritmo no estime como más relevantes unos datos que otros. Los datos escogidos para entrenar el algoritmo son los relativos a China, Italia y España, dado que son los países donde el contagio ha tenido mayor relevancia y los datos que atañen al confinamiento son fáciles de conseguir.

Antes de aplicar el algoritmo, necesitamos reducir el número de factores. Nosotros, a ojo, hemos decidido que estos factores son relevantes, pero no hemos hecho ningún cálculo fuera de leer artículos y suponer que pueden ser útiles. Para ver su posible utilidad, usamos una herramienta llamada ‘SelectFromModel’, que, dado un algoritmo propio de sklearn, decide cuáles de los factores de nuestra ‘x’ (los factores a partir de los cuales queremos predecir) son mejores para predecir nuestra ‘y’ (el valor que queremos predecir). Para estimar cuales de las x son más relevantes usamos el algoritmo ‘ExtraTreesRegressor’, que es básicamente un árbol de decisiones similar a un ‘Random Forest’

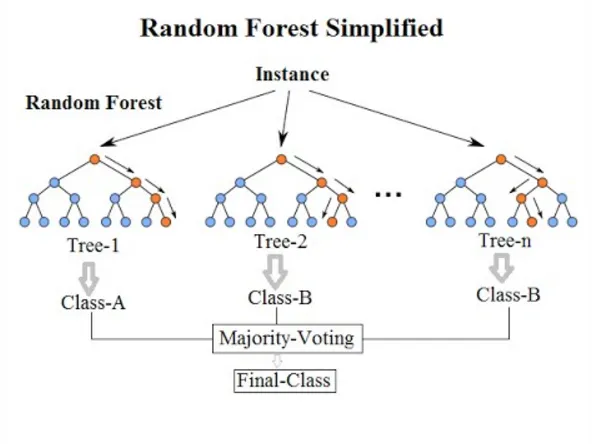
Una vez hemos pasado este algoritmo, tenemos nuestras ‘x’ en una dimensión menor (entre 8 y 5, dependiendo de cada caso). Pasamos estos datos por una red neuronal ‘LSTM’, la cual es una herramienta más potente que un árbol de decisiones, obteniendo ‘fits’ similares al siguiente (en muertes per million):

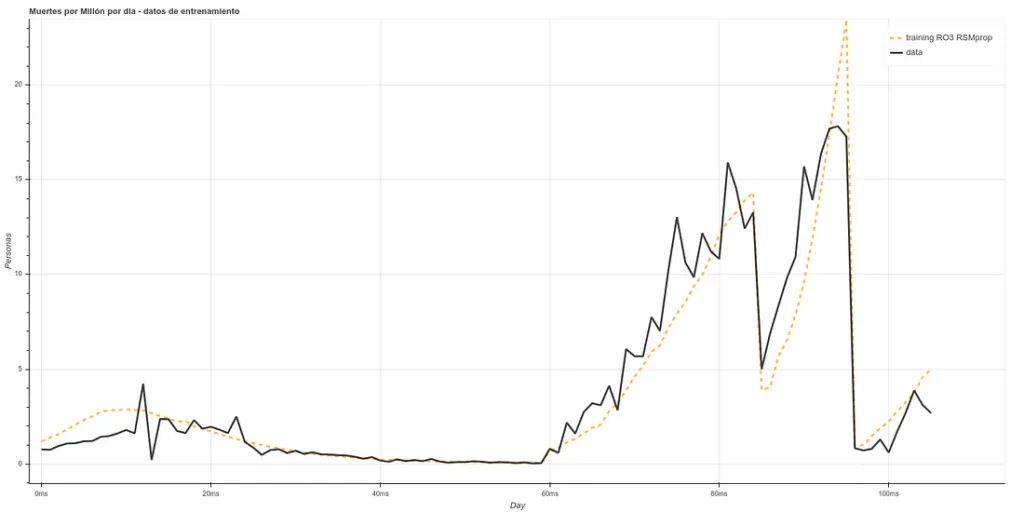
El training está compuesto por los datos chinos, italianos, españoles y parte de los ingleses ‘stackeados’ uno detrás de otro, empezando 20 días después del día 0. Como la predicción para un día X se basa en datos de, como poco, X-5, podemos hacer estimaciones a 5 días vista (o más, si hacemos nuevas predicciones basadas en las pasadas, pero haremos únicamente de 5 días por ahora).

La estimación para los siguientes 5 días en UK sería la siguiente:

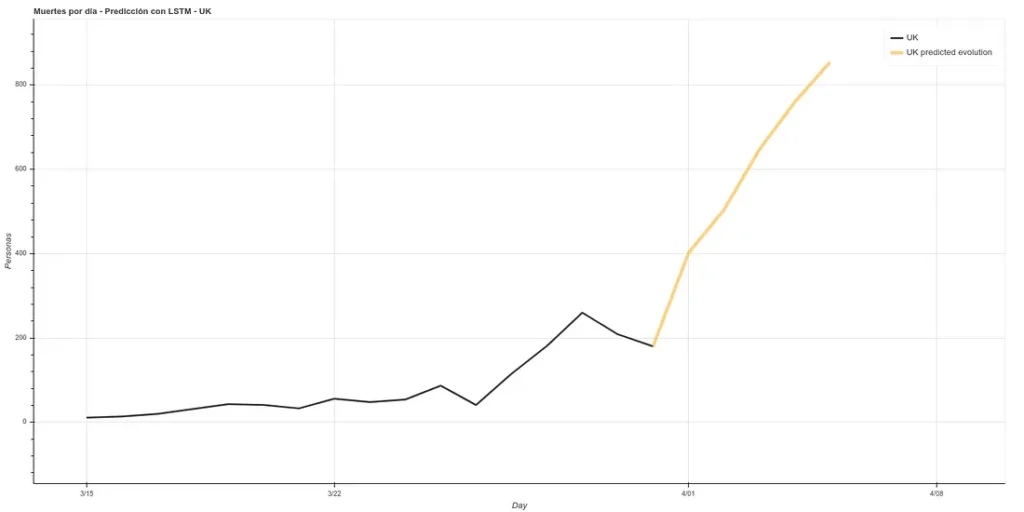
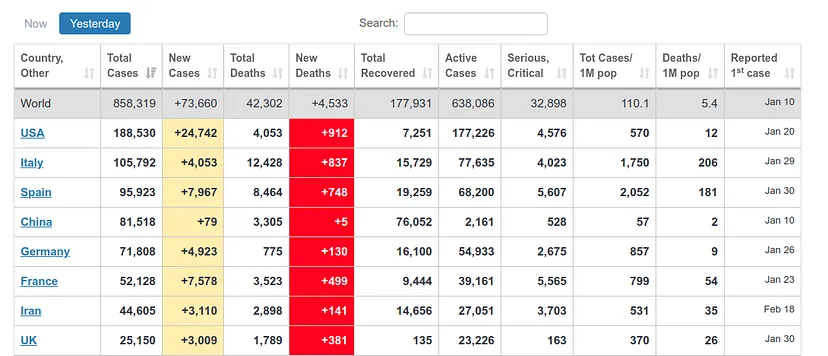
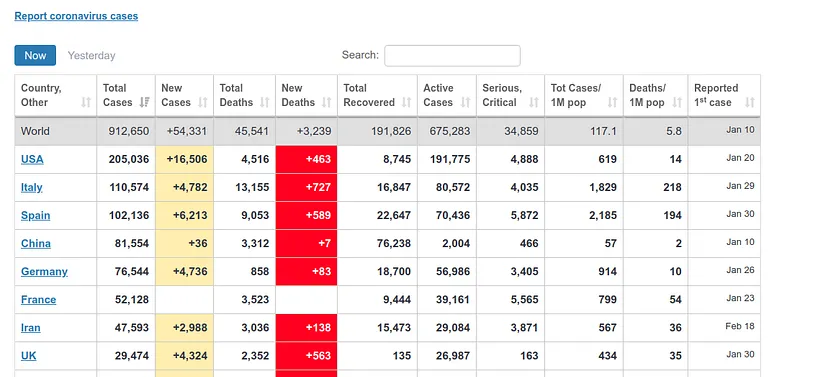
Estima unos 400 muertos para el 1 de Abril, día en que estoy escribiendo este artículo. Subida muy grande, viendo que el anterior máximo había sido de poco más de 200. Sin embargo, la actualización de los datos de la ECDC contabiliza los datos pasados un día, esto es, los datos que presentará hoy son los datos que cada país publicó el día anterior. Por tanto, podemos ver si nuestra predicción ha sido buena. En https://www.worldometers.info/coronavirus/ podemos ver una tabla de los datos actualizados para cada país, y podemos ver que para UK ayer (nuestro dato predecido de hoy) hubo 380 muertos y hoy (nuestro dato predecido de mañana) hubo 563 muertos, lo cual se corresponde bastante bien con nuestra predicción.

Disclaimer: no somos expertos, por lo que podemos haber incurrido en errores evidentes en la parte epidemiológica, que el modelo ‘fittee’ no quiere decir que sea fiable, tanto más cuando esto ha sido hecho en unas pocas tardes.

El notebook usado para alcanzar estos resultados es el siguiente: https://github.com/ATG-Analytical/COV-19-forescast/blob/Develop/WhoDataset%20-%20LSTM%20-%20SelectFromModel%20-%20Prop.ipynb

Explicación ‘técnica’ en inglés de los pasos seguidos para hacer dicho notebook aquí: https://medium.com/atg-analytical/using-lstm-to-get-a-coronavirus-evolution-prediction-on-uk-data-8830f65a3c31

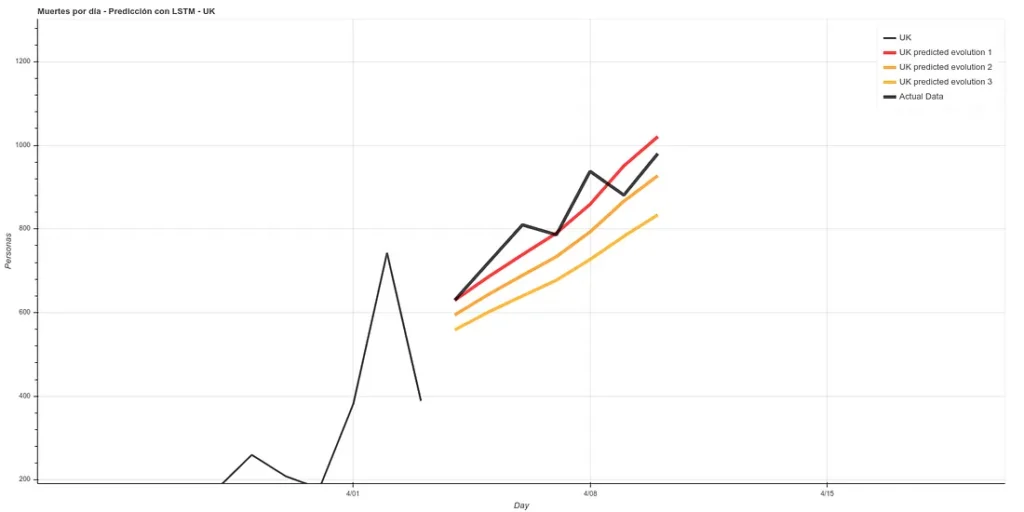
Update: Predicción a 7 días en UK. Son 3 modelos que tienen aproximadamente la misma precisión sobre la fase de training (~16%). Personalmente me creo más la predicción 1 pero aquí pueden ver las 3.

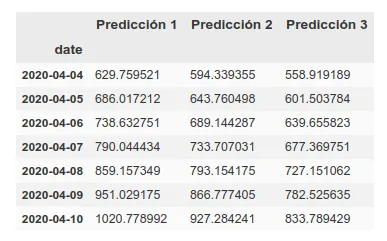
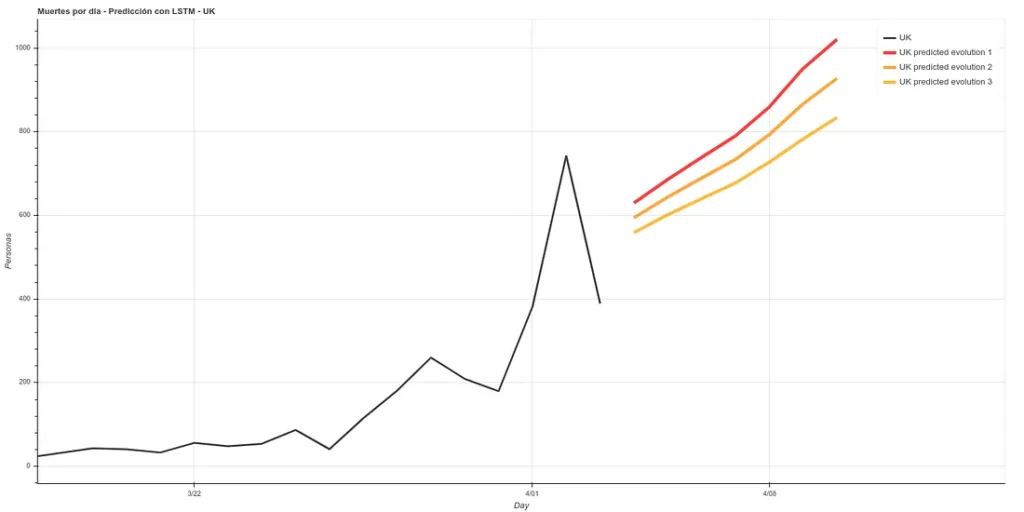
7 días después (a 11 de Abril actualizo), podemos ver los resultados de esa predicción. Los resultados son bastante buenos, siguiendo la ‘Predicción 1’.

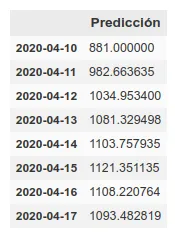
He añadido una pequeña actualización al código, cambiando los datos de muertes absolutos, haciendo un rolling average de 3 días, de forma que se eliminen picos para cada caso. Un rolling average de 3 días sería básicamente que para el dato de cada día se realiza la media usando el dato actual más los de los días alrededor, con lo que se suaviza la curva, lo cuál podría facilitar la predicción. Aquí la nueva predicción:

Esta predicción tiene un error medio en el training del ~7%

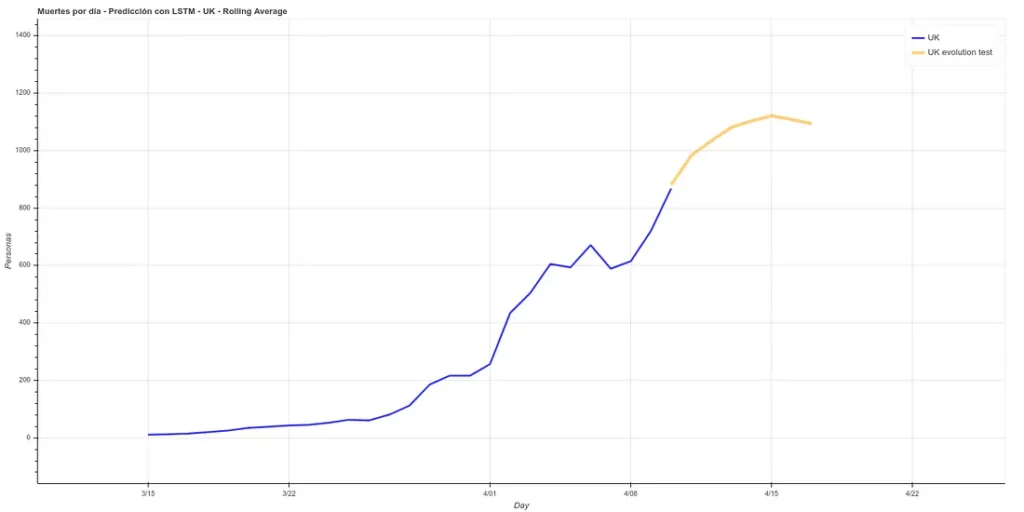
Por otro lado, mantenemos la predicción con los mismos métodos que usamos anteriormente, que han mejorado su precisión al tener más datos de training hasta aproximadamente el 6%. Esta predicción da una proyección más alta aunque también coincide con la del rolling average en una llegada al pico de muertes la semana que viene.

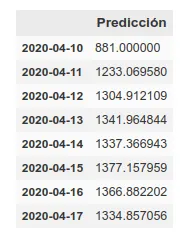
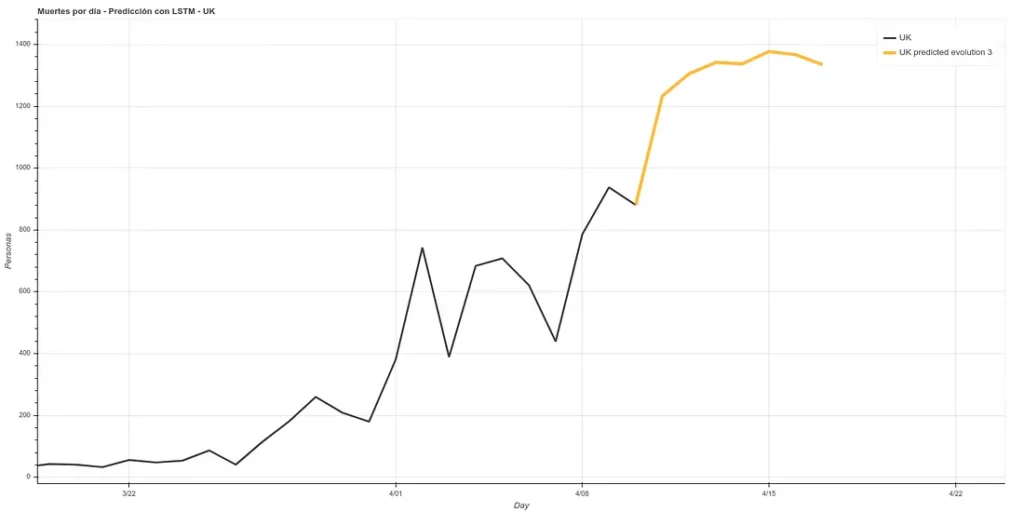
La gráfica con ambas predicciones quedaría así.

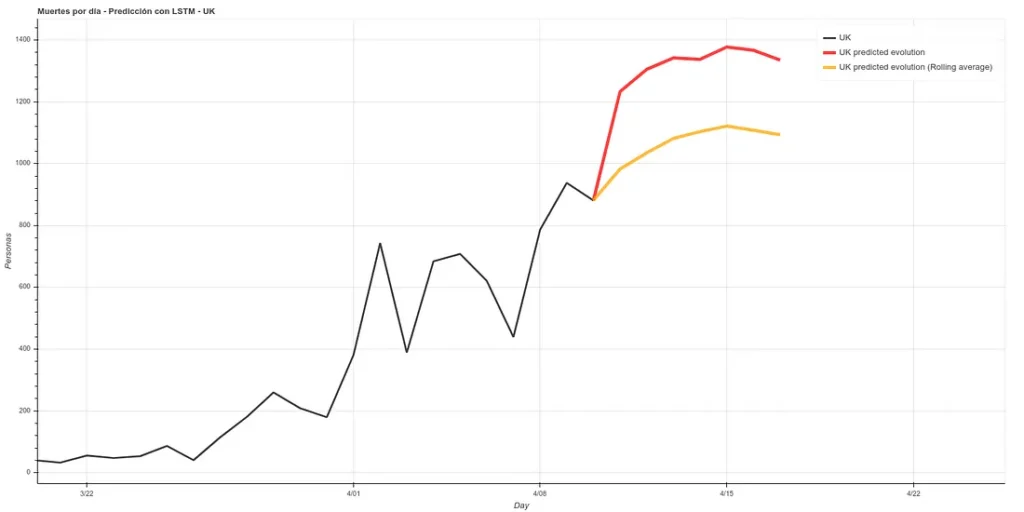
Nota: los datos de estas gráficas respecto a los que añadí anteriormente son diferentes. Esto es porque los datos que mostré antes para ilustrar la comparativa entre nuestra predicción y los datos reales los recopilé manualmente desde la cuenta oficial del ministerio de Sanidad británico (https://twitter.com/DHSCgovuk) mientras que los datos que uso para realizar la nueva predicción son los datos de la ECDC, que como comenté anteriormente durante el artículo, suelen tener cierto retardo a la hora de actualizarse.