Desde el inicio de esta pandemia, muchas preguntas e interrogantes se han hecho a cierto respecto. ¿Se reducirán sus efectos durante los meses de Verano? ¿Tiene algún efecto el calor sobre este virus como lo tiene sobre otros virus?

Podemos encontrando tanto declaraciones de Donald Trump donde habla de un segundo rebrote en Otoño (suponiendo que durante Verano no habrá o se reducirán muchos los contagios) como artículos de la BBC o El País hablando este tema, queriendo creer que el Verano y el calor aplacará el virus.

Pero bueno, ¿cuánto de cierto hay en esto? Podemos ver varios estudios hablando de estos temas. Primero, lo más básico. Estudio realizado por facultativos de la Universidad de Marsella (Pastorino et al.) donde realizan diferentes tests en laboratorio comprobando la resistencia del virus a grandes temperaturas . Este estudio es un pre-print (no ha sido revisado por un igual) pero no sirve por ahora para ilustrar que, a priori, las altas temperaturas de Verano no matarán al virus. Los resultados muestran que el virus tiene una resistencia al calor bastante fuerte y necesita varias horas de muy alta temperatura para morir.

Por otro lado, tenemos un extensivo informe chino relacionando contagios con climatología, con resultados negativos en cuanto a esta correlación. Sin embargo, si podemos poner una pega a este informe es precisamente que son datos chinos. El enorme despliegue que realizó China para detener al virus, incluyendo confinar completamente Wuhan llevó a que el virus se extendiera de forma muy limitada por su geografía, con lo creo que es difícil saber con esos escasos datos la posible correlación.

También tenemos un pequeño informe del AEMET donde se hace una tímida correlación entre la temperatura media y la cantidad de contagiados en España. Podemos ver la gráfica resultado en la siguiente figura.

Ahora bien, con la gran cantidad de datos con los que ya contamos, podemos hacer un nuevo análisis. Por supuesto, intentar correlacionar directamente la temperatura con la cantidad de contagios sin tener en cuenta otro tipo de factores no tiene mucho sentido. Por ello, para hacer un análisis rápido pensé que podía ser ideal utilizar datos americanos, donde el virus se ha extendido a gran velocidad sin demasiados impedimentos y los datos son fáciles de adquirir. Comparar diferentes países entre sí no me parece que tenga mucho sentido porque habrá muchos factores diferentes que expliquen la expansión de la pandemia como medidas previas, sanidad, etc. Sin embargo centrándonos en un único país con medidas más o menos uniformes, con una gran extensión y población podemos obtener unos resultados interesantes, por lo que USA parece ideal para esto. Además, con respecto a los datos españoles, usaremos métodos de machine learning para ver más de un factor en la relación, ya que evidentemente Asturias y Madrid (por ejemplo) no tienen la misma densidad de población aunque puedan tener temperaturas parecidas, lo cuál debe de ser un factor relevante.

Por un lado, los datos de muertos por COVID según el estado. Como ya comentamos en el anterior artículo de este blog, creo que utilizar los datos de muertos es más útil que los datos de contagios, por lo que usaré esa medida para ver el avance de la pandemia. Obtengo esos datos de este git propiedad del NY Times, que contiene también los datos de muertos a nivel estatal y por ‘county’.

Los datos sobre la densidad de población y la población total los encontramos aquí: https://worldpopulationreview.com/states/

Mientras que los datos de temperatura del último mes los podemos encontrar aquí: https://www.ncdc.noaa.gov/cag/divisional/mapping/110/tavg/202003/1/value

Como este artículo será más corto explicaré un poco los pasos que sigo para conseguir el formato adecuado para los datos.

* Preparación de los datos

COVID

Como comentamos antes, usamos los datos por estado, utilizando ‘pandas’. Quiero unicamente los datos de hoy (día que escribo inicialmente este artículo, 22 de Abril), así que elijo los correspondientes a la fecha y a continuación utilizando la herramienta ‘iloc’ de pandas, elijo las columnas 1 y 4, las correspondientes al estado y las muertes.

a = pd.read_csv(‘covid-19-data-master/us-states.csv’)
states = a[a[‘date’]==’2020–04–22']
states = states.iloc[:,[1,4]]

Población

De nuevo, leemos el ‘csv’ utilizando pandas y elegimos los datos que nos interesan. En este caso son las columnas 1, 2 y -1, correspondientes a estado, población y densidad de población, a las que además cambiamos el nombre para que tengan nombres homologables con el anterior DataFrame.

data = pd.read_csv(‘data.csv’)
data = data.iloc[:,[1, 2, -1]]
data.columns = [‘state’, ‘population’, ‘population density’]

Temperatura

Este CSV es algo más complicado, pero nada que no podamos solucionar.

Podemos ver como hay varias ‘Location’ para cada estado, 8 solamente para Alabama. Esto lo podriamos solucionar de varias maneras, pero como buscamos solucionar este problema de forma meramente orientativa y por curiosidad no nos vamos a complicar demasiado. Simplemente escogeremos una de las filas por estado para realizar el cálculo, para ser exacto, el ‘CD 1.’ de cada uno de los estados.

Para ello, iteramos sobre esa columna ‘Location’ y creamos una lista nueva separando quitando a cada estado el ‘CD 1.’, para, a continuación, hacer esa lista la columna ‘Location’.

newloc = []
for i in temp['Location'].values:
    newloc.append(i.split(' CD 1.', 1)[0])
temp['Location'] = newloc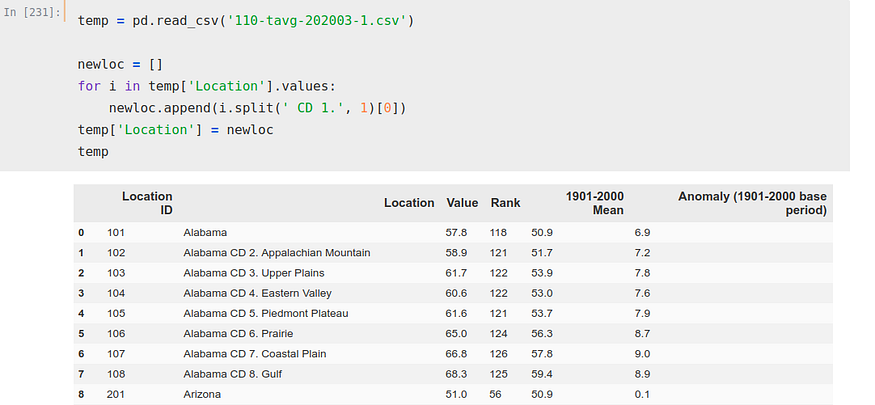

Ahora, iteramos de nuevo, esta vez sobre dos columnas, índice y ‘Location’. Con esta iteración hemos creado una lista donde hemos guardado los índices que queremos utilizar para obtener nuestro DataFrame.

indexxxx = []
for i, j in zip(temp.index, temp['Location']):
    if 'CD' not in j:
        indexxxx.append(i)

Ahora, simplemente copiamos esos índices, utilizando ‘iloc’ de nuevo para seleccionar las filas que queremos y las columnas (1 y 2, las correspondientes a localización y temperatura media). También cambianmos el nombre de las columnas, de forma que queden en el mismo formato que nuestros otros dos DataFrames.

temp = temp.iloc[[0, 8, 15, 24, 31, 36, 39, 41, 48, 57, 67, 76, 85,
 94, 103, 107, 116, 119, 127, 130, 140, 149, 159, 165, 172, 180,
 184, 186, 189, 197, 207, 215, 224, 234, 243, 252, 262, 263, 270,
 279, 283, 293, 300, 303, 309, 319, 325, 334], [1, 2]]temp.columns = [‘state’, ‘temperature’]

Ya tenemos todas los DataFrames preparados, por lo que podemos unificarlos todos en uno y realizar los cálculos. Además, realizamos una nueva modificación, sustituyendo en el DataFrame las muertes por muertes por Millón.

merge1 = states.merge(data)
merge2 = merge1.merge(temp)
merge2['deaths per M'] = merge2['deaths']/merge2['population']*1000000
merge2.drop('deaths', axis=1, inplace=True)

Regresión

Ahora, podríamos dividir nuestros datos en ‘training’ y ‘test’ pero creo que en este caso no es lo más útil, dado que no estamos haciendo una regresión con datos temporales. Por ello, creo que lo ideal en este caso es usar ‘cross-validation’. Este método divide el dataset en x partes diferentes, de forma que el training entrena en x-1 y testea su validez sobre 1 de esas partes. Con ese ánimo, realizamos una división en 5 partes de este dataset, utilizando el ‘regressor’ ExtraTreesRegressor.

from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_validateETR = ExtraTreesRegressor()X = merge2.iloc[:,[1, 2, 3]]Y = merge2.iloc[:,[4]]cv_results = cross_validate(ETR, X, Y, cv=5, scoring='neg_mean_absolute_error')

Con lo que obtenemos el siguiente mean absolute error (en negativo, función de sklearn)

Podemos ver, si usamos la herramienta ‘feature importances’, la importancia que está dando a cada factor el algoritmo una vez está ‘fitteado’.

ETR.fit(X, Y)from matplotlib import pyplotpyplot.bar(X.columns, ETR.feature_importances_)
pyplot.show()

Filtrado de datos

Sin embargo, no hemos filtrado demasiado, lo cuál suele ser el principal factor para obtener un buen resultado en este tipo de trabajos. Tenemos Nueva York, que al contar el estado entero en vez de únicamente la ciudad, da una densidad de población bastante menor a pesar de que tiene la zona más densamente poblada del país junto a la mayor tasa de muertos por millón, por lo que puede estar llevando a confusión al algoritmo. Podría ser beneficioso separar los datos de Nueva York ciudad y sus suburbios de los datos del resto estado, pero no nos tomaremos ese trabajo para no cambiar el método. Filtrando y dejando fuera Nueva York, realizamos de nuevo estos cálculos

merge1 = states.merge(data)
merge2 = merge1.merge(temp)
merge2['deaths per M'] = merge2['deaths']/merge2['population']*1000000
merge2.drop('deaths', axis=1, inplace=True)
merge2 = merge2[merge2['state']!='New York']

Realizando el mismo algoritmo de nuevo…

from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_validateETR = ExtraTreesRegressor()X = merge2.iloc[:,[1, 2, 3]]Y = merge2.iloc[:,[-1]]cv_results = cross_validate(ETR, X, Y, cv=5, scoring='neg_mean_absolute_error')

Vemos como el error ha disminuido considerablemente

Mientras el factor de importancia que el algoritmo da a la temperatura ha aumentado con respecto a la población total, aún así sigue siendo bastante menor a la densidad de población como es normal.

Por supuesto, estos resultados pueden ser meramente casuales, correlación no implica causalidad pero es como poco curioso esta correlación y un factor que se podría estudiar.

La gráfica producto de correlacionar temperatura contra muertes una vez eliminado Nueva York es la siguiente:

Y si realizamos una nueva gráfica, dividiendo temperatura entre densidad de población, por correlacionar de forma simple ambos ambos conceptos, vemos lo que parece una gráfica con una correlación bastante clara. A mayor temperatura y menor densidad de población el ratio de muertes baja mucho, mientras que todos los casos de mortalidad alta ocurren en estados de baja temperatura y alta densidad de población.

Si hacemos una escala logarítmica para visualizar la curva mejor obtenemos de hecho una curva muy similar a la obtenida por el AEMET, observable en la siguiente gráfica, donde además los datos han sido normalizados.

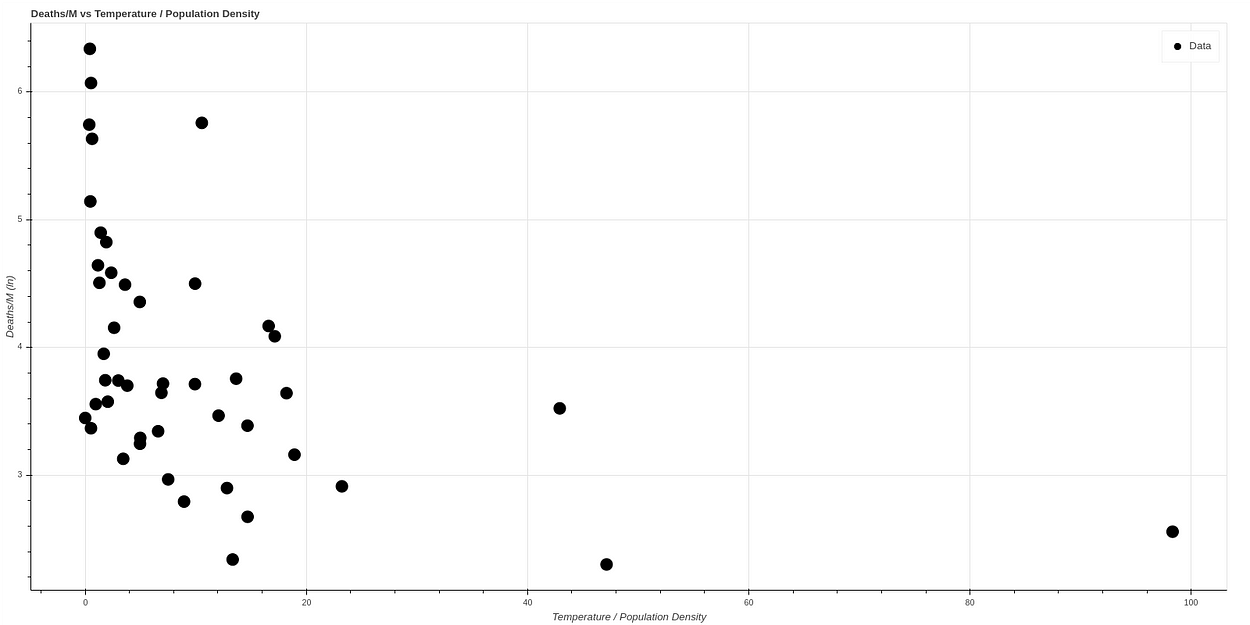
Fitteando el algoritmo sobre los primeros 41 estados y testeando sobre los 7 obtenemos un resultado similar a este:

Se pueden encontrar todos estos cálculos en nuestro git: https://github.com/ATG-Analytical/COV-19-forescast/tree/develop

Ha pasado un mes desde que hice este análisis, ‘plotteando’ de nuevo un mes después (23 de Mayo) obtenemos unos datos muy similares, con lo que parece confirmarse esta teoría. Aquí podemos ver una comparativa entre ambos datos.